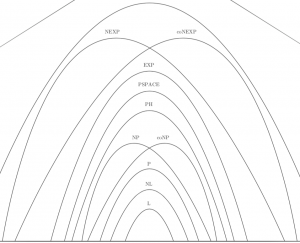
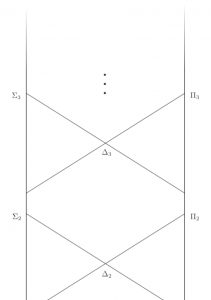
One of the joys of philosophy is seeing how things “hang together in the broadest sense” (Sellars, Philosophy and the Scientific Image of Man, p.361). Information graphics can be a powerful tool do just this.
Bomze’s Classification of 3×3 Games Under the Replicator Dynamics
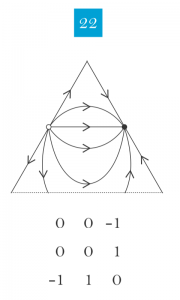
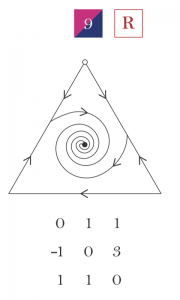
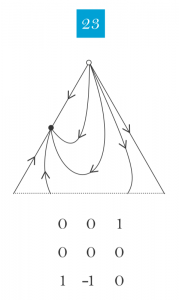
The replicator dynamics is the “first and most important model of evolutionary game theory” (Cressman, The Replicator Equation and Other Game Dynamics, p.1081). This dynamics isolate the qualitative influence of selection on evolution, and capture the idea that types that are more fit than the population average fitness grow in proportion, while types that are less fit than average shrink in proportion. When there are three types in a population, there are 49 logical possibilities for the qualitative dynamics of evolution. These dynamics, their stability properties, and relationship to the standard equilibrium concepts (ESS, NSS, ESSet) are captured in this visualization.
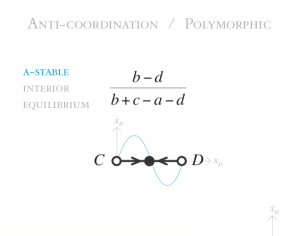
Classification of 2×2 Games Under the Replicator Dynamics
When there are two types in a population, there are 5 logical possibilities for the qualitative dynamics of evolution. These include the famous Prisoner’s Dilemma, Prisoner’s Delight, Stag Hunt, and Hawk-Dove games. In the simple case of two of population composed of types, the ESS concept captures all and only the evolutionarily significant outcomes of the dynamics. These dynamics and their stability properties are captured in this visualization.
PAC Learning, Occam’s razor, and the Transfinite Hierarchy (w/ Daniel Herrmann)
Computer scientists have provided a distinct justification of Occam’s Razor. Within the context of the probably approximately correct framework, Blumer et al. (1987) prove a theorem they claim demonstrates that we should favour simpler hypotheses in our inquiry, and thus that they have vindicated Occam’s Razor. Daniel Herrmann demonstrates that simplicity is not what is doing the work in their theorem; what is really doing the work are additional inductive assumptions. With such assumptions, many different methods can learn without relying on any notions of simplicity. Thus, the theorem cannot be a justification of Occam’s Razor.