“The mathematical sciences particularly exhibit order, symmetry, and limitation; and these are the greatest forms of the beautiful.”
—Aristotle, Metaphysica, 3-1078b
Scientific philosophy can involve the creation and analysis of mathematical and computational models. For my research, these may be models of optimal learning, decision-making, strategic behavior, evolution, network formation, and much else besides.
Below are a few of the models I’ve created for various projects. Their source codes are available at my GitHub page and are copyrighted under a Creative Commons share-alike license.
Modeling Interventions in Science
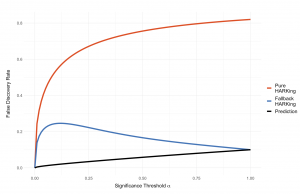
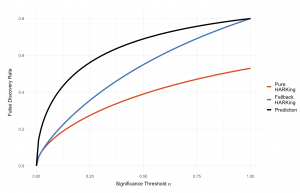
The modern sciences face a crisis of credibility in which we have become aware that our research practices, standards of evidence, and incentive structures have led to less reliability in our scientific findings than we would wish.
To address this challenge, prominent changes have been proposed: among these are redefining statistical significance, promoting preregistration, and incentivizing the publication of null results.
Thi model explores the potential impacts of such interventions—given varying background assumptions—on measures of the reliability and fecundity of scientific production.
Bayesian Learning with Conformity on Social Networks
One of the most important domains of social inquiry is that of broad public discourse. Which social policy will lead to better outcomes? Which political candidate is more qualified for office? Typically, public discussion on such questions of import is influenced by the human tendency of conformity. Individual decisions are informed and influenced by peers.
This model explores how social networks, in tandem with conformity bias, can influence the flow and reliability of information in social learning.
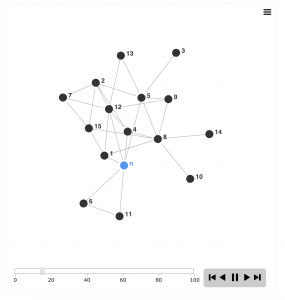
Self-Assembling Networks with Reinforcement Learning
Social epistemology needs to study how information is transmitted through a social network. In order to do this, it must explore how social networks develop in tandem with the communication they enable.
This model explores how an epistemic network might self-assemble as heterogeneous agents investigate nature and each other.
Tragedies of the Commons
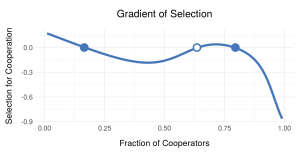
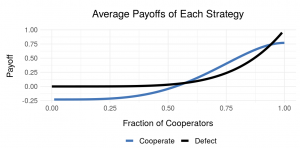
From global warming to nuclear weapons proliferation, how to deal with collective action may be formulated in terms of a public goods game of cooperation. Human cooperation in public goods problems is threatened by the immediate advantage of free riding which can lead the population into the tragedy of the commons.
This model explores the effects of the perception of risk and magnitude of the consequences of failure to cooperate, cost of cooperation, and cooperative group size on N-person public goods games.
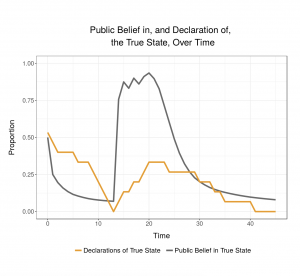
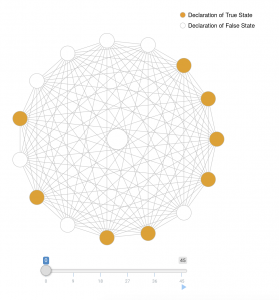
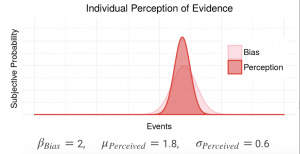
Reporting, Bias, and Belief Distortion
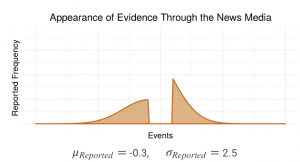
The news media provides us with information about what’s going on in the world. The news is also subject to several characteristic distortions. Only sufficiently unusual or extreme events tend to be reported. Events which are reported tend to be exaggerated in intensity. Norms of ‘fair-and-balanced’ reporting can give equal weight to positions with asymmetric evidential support. These distortions interact with the individual tendency to differentially accept news congenial to prior beliefs and reject news uncongenial to prior beliefs.
This model explores how individual confirmation bias in tandem with selective or distorted representations of events by the news media can lead to individual belief polarization.
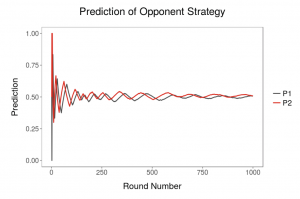
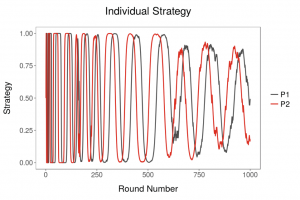
Rationality and Prediction in Games of Uncertain Information
The Nash equilibrium concept has come to be central to game theory, economics, and other social sciences. A long-standing open question in the theory of games is the extent and condition under which we may expect rational agents to play the Nash equilibria of games. In The Impossibility of Prediction the Behavior of Rational Agents (2001) Foster and Young prove an impossibility theorem that demonstrates the non-robustness of Bayesian learning in justifying Nash equilibrium play. They show that in near-zero-sum games, agents cannot be both rational and also learn to accurately predict the strategies of their opponents.
This model demonstrates the essential tension between rationality and prediction, and how we might resolve it.
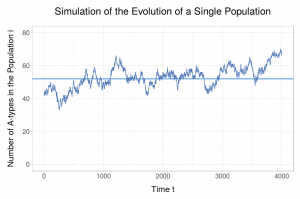
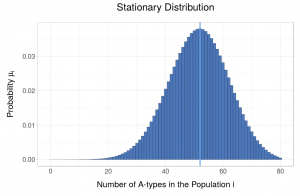
Frequency-Dependent Moran Process and Stability Concepts
The Moran process is “the simplest possible stochastic model [with which] to study selection in a finite population” (Nowak, Evolutionary Dynamics: Exploring the Equations of Life, p.94). This model allows one to examine the evolutionary process when there are two interacting pheno- or genotypes within a fixed finite population.
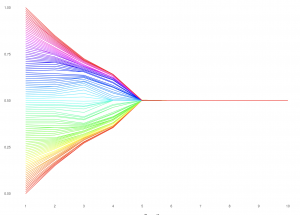
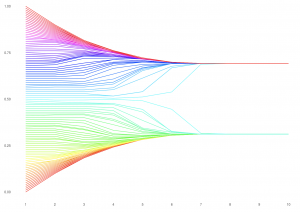
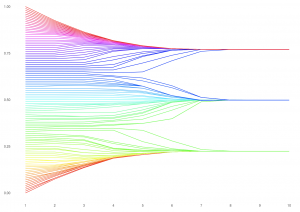
Bounded Confidence Model of Opinion Dynamics
When does opinion formation within an interacting group lead to consensus, polarization, or fragmentation? The Hegselmann-Krausse bounded confidence model of opinion dynamics offers one attempt to explore this question.
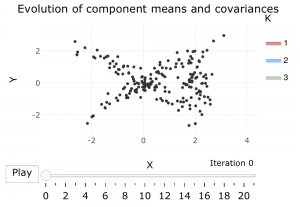
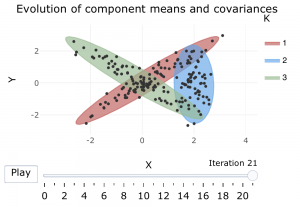
EM Algorithm for Gaussian Mixtures
A fundamental problem in inductive inference is how to learn the structure of unlabeled data. This is known as unsupervised learning in machine learning and clustering in statistics.
This model demonstrates an important technique for dealing which such problems: the estimation-maximization (EM) algorithm. When data are missing, or analytic solutions are not available, the EM algorithm can provide an iterative approach to a maximum likelihood solution.
